p(xt | z1:t-1) = f p(xt | xt-1, z1:t-1)P(xt-1 | z1:t-1)dxt-1

根据马尔科夫假设，当前的状态只与前一时刻的状态有关，与历史观测值无关，通常去掉,z1:t-1，f表示积分

查普曼-科莫高洛夫方程：

p(xt | z1:t-1) = f p(xt | xt-1)P(xt-1 | z1:t-1)dxt-1

 

P(y,z | x) = P(y | z,x)*P(z |x)，可以这样理解：P(y,z) = P(y | z)*P(z)，然后两边加入条件x即可。

P(y| x) = f  P(y,z | x) dz，看成是y,z的联合分布对z积分即是边缘分布

而 f  P(y,z | x) dz = f  P(y | z,x)*P(z |x) dz

 

 

---------------------

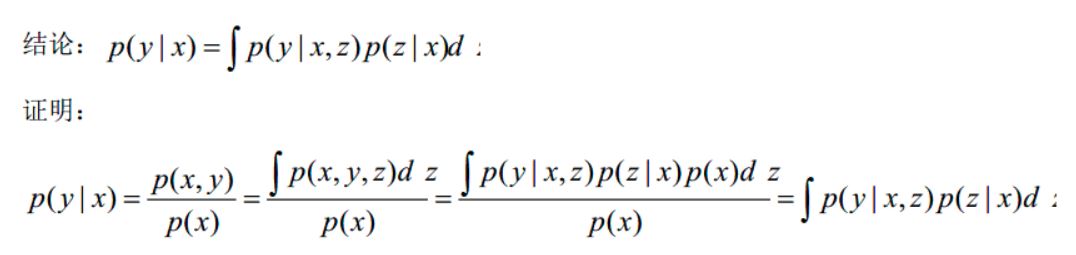
作者：yysunlife

来源：CSDN

原文：https://blog.csdn.net/yang090510118/article/details/38427061